Adinkra Codes: An Elementary Introduction

1. How Adinkra symbols, quantum physics, and error-correcting codes came to be associated together

Let’s begin by giving a short summary of how the unlikely alliance between Adinkra symbols, steeped in centuries of African tradition, supersymmetry, a pet theory of keen theoretical physicists, and error-correcting codes, a bedrock of modern information and communications technology came to be.

Despite the history of Adinkra as visual symbols for depicting aphorisms and communicating deep truths, the connection to quantum physics and communications technology seems a rather unlikely development. However, Adinkra has become a handy metaphor for a geometric way of encoding the mathematical relationships between fundamental particles in supersymmetry classes.

2. What is supersymmetry?

Supersymmetry is a theory in physics that captures the correspondence between two dissimilar classes of subatomic particles—matter particles on one hand, and force-carrying particles on the other. In what is known as the Standard Model of particle physics, the matter particles are all fermions while the force-carrying particles are all bosons. However, supersymmetry, usually abbreviated as SUSY, breaks this rule.

In SUSY, every particle is associated with a supersymmetric partner that belongs to its opposite class. Hence, the electron, which is a matter particle and therefore a fermion, is associated with a sypersymmertic partner called a selectron (that is, a supersymmetric electron) that is a boson. One motivation for this is the extension of the particle-antiparticle duality that exists for particles in the Standard Model to SUSY.

3. Adinkra encode the essence of SUSY equations

Typically, physicists describe these relationships between particles with equations. However, S. James Gates and his collaborators (including Charles Doran, Michael Faux, Tristan Hubsch, Kevin Iga, Greg Landweber, and others) found that in addition to the traditional equations that are used to describe such relationships, they could also use diagrams, akin to how Feynman diagrams are used in quantum electrodynamics, to represent the relationships between these particles. The structure of the diagrams that emerged as they embarked on this voyage prompted their christening as Adinkra, taking inspiration from Adinkra symbols which are also used to represent complex systems of thought, belief, and practice among their originators, the Gyaamans and Akans of Ghana and la Cote d’Ivoire.

Thus, in the context of theoretical physics, we may define Adinkra as geometric objects that represent mathematical relationships between supersymmetric particles. (Gates) They encode the essence of the equations that represent the relationships between these particles.

4. The rules of Adinkra

Figure 1: Two Adinkra formed from squares along with the equations that the Adinkra at the bottom left represents. Source: On Being

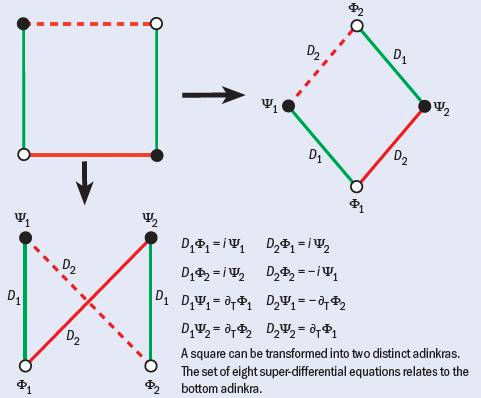
1. All Adinkra start from squares, cubes, and their higher-dimensional generalizations, known as hypercubes. To get Adinkra, we enhance the starting cube following some additional rules:
2. Each vertex of the cube must have a black dot or a white dot but this must be done in such a way that black dots are only connected to white dots and white dots are only connected to black dots.
3. The links or edges must be assigned directions. We do this by assigning them colors. All links that point in the same direction are given the same color and links that point in different directions must have different colors.
4. We assign an “edge parity” to each link. That is, each link can be drawn as a solid line or a dashed line but it must be done in such a way that every loop with two colors must contain an odd number of dashed links.
5. Dots with different colors are not allowed to be at the same level or height. That is, if a level has a white dot, all the other dots at that level must be white and vice versa.

5. The utility of Adinkra

If theoretical physicists already have the equations that characterize the relationships they are interested in, why are they bothering themselves with complex Adinkra with all these rules? This may seem surprising at first till one realizes that mathematicians and scientists are in the habit of translating problems from lesser-understood domains to better-understood ones in order to exploit the structure and understanding of the better-understood domains to draw useful complementary inferences.

Adinkra diagrams simplify the characterization of the relationships between the particles of interest and make it possible to bring our visual and geometric intuitions to bear on the domain of SUSY. Further, by translating the essence of their discoveries into other flavors of mathematics (e.g., graph theory in this case), they widen the net of mathematicians and scientists who can readily appreciate their findings and potentially contribute to it. As Gates notes, such diagrams are more than mere pictures as they can lead to new understandings of what is being studied.

Figure 2: Adinkra decomposed into smaller Adinkra. Source: On Being

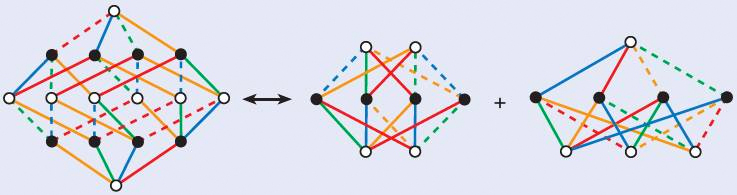
As an example, the researchers noticed that some Adinkra could be broken up into two smaller parts, both of which were also Adinkra. Further, they found that by a process of folding, compression, and coalescing of the dots and links of Adinkra, other Adinkra could be formed. Though not all such manipulations of Adinkra result in new Adinkra, by assigning binary words to the dots in Adinkra and following a specific process of transformation, the researchers found that the SUSY property could be reliably preserved. This process is elaborated in Section 8. From this discovery, they noted that the equations which Adinkra represent exhibit properties held by a specific class of error-correcting codes known as doubly even self-dual linear binary error-correcting block codes. As this was a completely unexpected result that did not arise from studying the equations directly but from studying their alternative representations as Adinkra, this alternative mode of representation has yielded an unexpected payoff.

6. A detour into the land of error-correcting codes

Error-correcting arise from a pretty natural desire: During communication between two points, let’s call them the sender and the receiver, can the receiver guarantee that the message he has received is the one the sender sent?

When the receiver cannot detect nor correct errors in the message he has received, the message loses its usefulness. Digital communication occurs through the transmission of strings of zeroes and ones, called bits. Thus, whatever needs to be transmitted eventually needs to be converted into its binary equivalent for the communication to proceed. However, as these strings of bits are being transferred, errors do occur due to the unreliability of the transmission channels. Thus, it becomes necessary to be able to detect when there have been errors and also to correct some of them. That is where error-correcting codes come in.

7. Repetition codes: a simple example of error-correcting codes

A simple example of an error-correcting code is a repetition code. In such a code, instead of simply sending the string of zeroes and ones we want to transmit, we send a padded string in which we repeat each digit a pre-determined number of times. So, for example, to transmit the string 01011, we would instead transmit 000111000111111. In this new string, each digit in the original string is repeated three times. 0 becomes 000, 1 becomes 111, all the way to the end.

Now, suppose the message is corrupted while being sent, that is, a 1 changes to a 0 or a 0 changes to a 1. In the case where the original message is sent, we have no way of knowing if any of the bits have been flipped. But if one error occurs in the padded string, we can know because the other bits will reveal it.

If instead of receiving 000111000111111, which is the uncorrupted message, we receive 010111000111111, in which the second bit has been flipped, how are we going to know?

Since we know that each bit in the original string was repeated three times, we can break up our message into three-bit chunks, starting from the first one. Thus, 010111000111111 becomes 010 111 000 111 111. When we do this, we immediately see that there is a problem in the first group of bits. Instead of all of them being the same, we have two zeroes and one one. If our channel is reliable so that we know that very few errors are going to occur in the transmission of messages, we can confidently flip the 1 back to a 0 because we conclude that that one is probably corrupted. Thus, we are able to recover exactly what the sender sent.

Notice that in the case where we have two or more errors within a three-bit chunk, we cannot be sure exactly what has changed so we cannot correct errors even if we are able to detect them. Also, the repetition code we have just described is simple but not the most efficient. When we repeat each bit three times, only one-third of the message we end up sending is the actual message we wanted to send. The other two-thirds is just extra padding to ensure that we can detect errors when there aren’t too many of them. In practice, more sophisticated error-correcting codes are used to detect and correct more errors as well as to increase the efficiency of communication.

8. The relationship between Adinkra codes and error-correcting codes

Figure 3: Adinkra with dots coded with binary words. Source: On Being

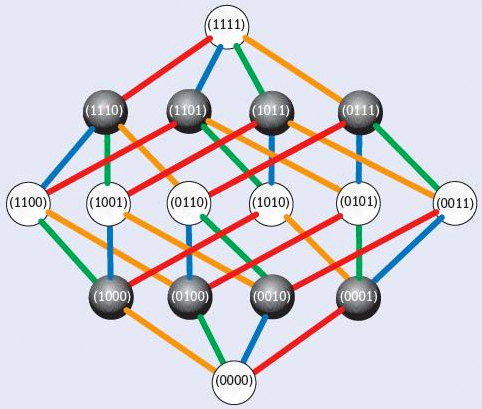
As already noted in Section 5, larger Adinkra can be transformed by a series of operations to obtain smaller Adinkra. However, for such transformations to preserve the SUSY property, the dots must first be coded with binary words in such a way that if two dots are connected, they can only differ in one bit. Then, dots can be fused by respecting the rule that the bitwise sum of their words must add up to a string of ones of length equal to the length of a word. In the example above, the bitwise sum of the words should be the string 1111. Hence, the dot at the top and the one at the bottom will be fused, as the bitwise sum of their words is 1111. All the other dots will be fused with their counterparts in the same way. Then the Adinkra in Figure 3 will become another Adinkra with 8 dots instead of 16.

As Gates notes, the process of coding dots in the fashion described and fusing them with the prescribed rule “happens to correspond to the simplest member of the family containing the check-sum extended Hamming code.” Thus, by following processes in coding theory, we unconsciously respect the principles of SUSY in theoretical physics—a rather unexpected development.

9. Conclusion

Students and admirers of Adinkra symbols and African philosophy will be pleasantly surprised to note the co-optation of their object of interest in an unexpected field of endeavor. This extension breathes new life into the ideas and concepts that Adinkra represent and amplifies the unifying themes of abstraction (of deep truths), compression (of complex messages that are difficult to express), and beauty (apparent in the elegance of the designs) that Adinkra collectively share.

10. References

1. Gates, S. J., Jr. (2012, April 8). Symbols of Power: Adinkras and the Nature of Reality. The On Being Project. Retrieved November 19, 2023, from https://onbeing.org/blog/symbols-of-power-adinkras-and-the-nature-of-reality/

2. Discussion on YouTube about whether our universe is a simulation